Digital logic circuit

논리 게이트

• 디지털 컴퓨터에서는 이진 정보는 물리량인 전압 신호를 이용하여 0과 1로 표현됨
  • (ex) 어떤 컴퓨터에서는 3V신호를 1로, 0.5V 신호를 0으로 나타냄.
• 이진 정보는 게이트(gate) 라고 불리는 논리 회로에서 행해짐.
• 게이트는 입력 논리 조건에 만족할때, 1 또는 0의 신호를 만들어냄.
  • 진리표에 나와있음.

부울대수

• 이진 변수나 논리 동작을 취급함.
• 변수는 A, B, x, y같이 문자로 표시.
• 세 개의 기본적인 논리 동작으로 AND, OR, 보수가 있다.
  • AND: ∧가 논리기호이고, 점( · )으로 연산 표시, 생략 가능
  • OR : 덧셈 기호(+)로 표시
  • NOT 연산 : 변수 위에 줄(-)을 그어 표시

• Ex) F = ABC+ABC’+A’C → F = AB+A’C

최소항, 최대항

• 최소항이란, 각 변수가 정확히 한 번씩 발생하는 N개의 개별 변수들의 곱(AND 연산)

minterm is the product (AND operation) of N distinct literals where each literal occurs exactly once.

• 최대항이란, 각 변수가 정확히 한 번씩 발생하는 N개의 개별 변수들의 합(OR 연산)

maxterm is the sum (OR operation) of N distinct literals where each literal occurs exactly once.

보수

complement

• 기호는 ‘이다.
• 반대되는 수… 보색도 반대인 색인 것 처럼
• 진법에 따라서 계산법이 다른데, 이진 변수를 A=0일때 보수취하면 A’=1 이런 원리.

수식의 보수

• De Morgan 정리를 이용해서 얻어낼 수 있음.
  1. 모든 OR 연산은 AND로, 모든 AND연산은 OR로 바꾸어 줌
  2. 각 변수를 보수화한다.

     예시:
     F = AB + C’D’ + B’D
     F’ = (A’+B’)(C+D)(B+D’)

맵의 간소화

• 진리표로부터 얻은 논리식을 간략히 하는 방법

Map 방식

• 부울 함수를 곧 바로 간소화할 수 있다.
  • Karnaugh Map 방식
  • Veitch Map 방식

Minterm

• 진리표에서 변수의 각 조합

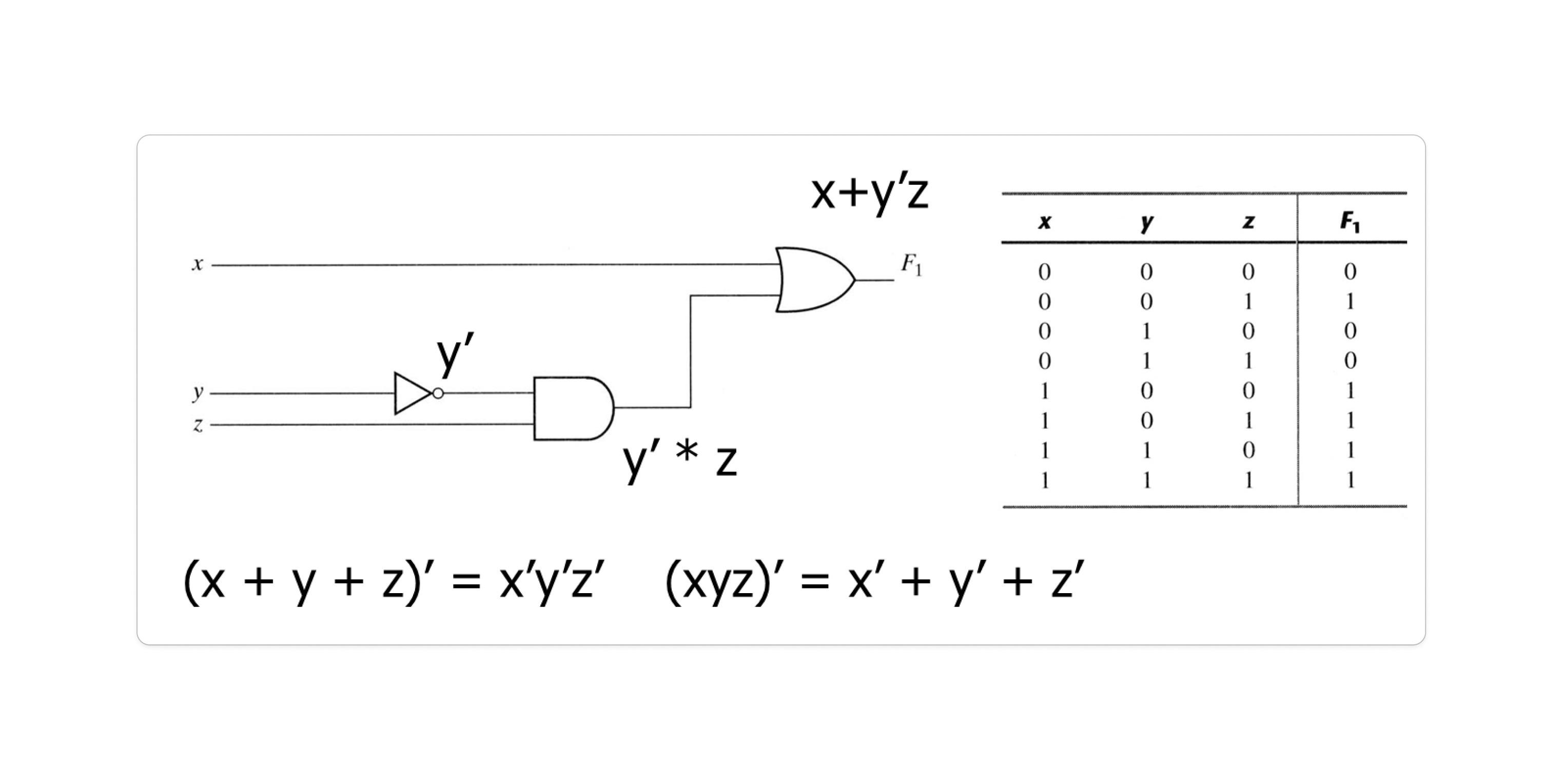
그림 1-3

• <그림 1-3>의 진리표는 8개의 minterm을 갖는다.

• n개의 변수가 있다면 2n 개의 minterm 이 존재

• <그림 1-3>의 진리표에서 출력F가 1이 되는 minterm 을 선택

• F(x,y,z)=∑(1,4,5,6,7)=x’y’z+xy’z’+xy’z+xyz’+xyz

K-Map

• 부울 함수를 간소화

• Map: 여러개의 사각형 구역, 각 사각형의 구역은 각각의 민텀을 표시함
• 함수가 1이 될때 논리 표현식의 출력이 1이 될때 해당 민텀의 구역에 1을 넣음
• 출력이 0이 될 때에는 해당 민텀의 구역에 0을 넣거나 안넣음. 보통 0을 안넣고 공백으로…
• 민텀 번호 (특징: 2진수)

K-Map의 구성

• 논리 표현식의 출력이 1이 될 때 해당 minterm 구역에 1을 넣는다.

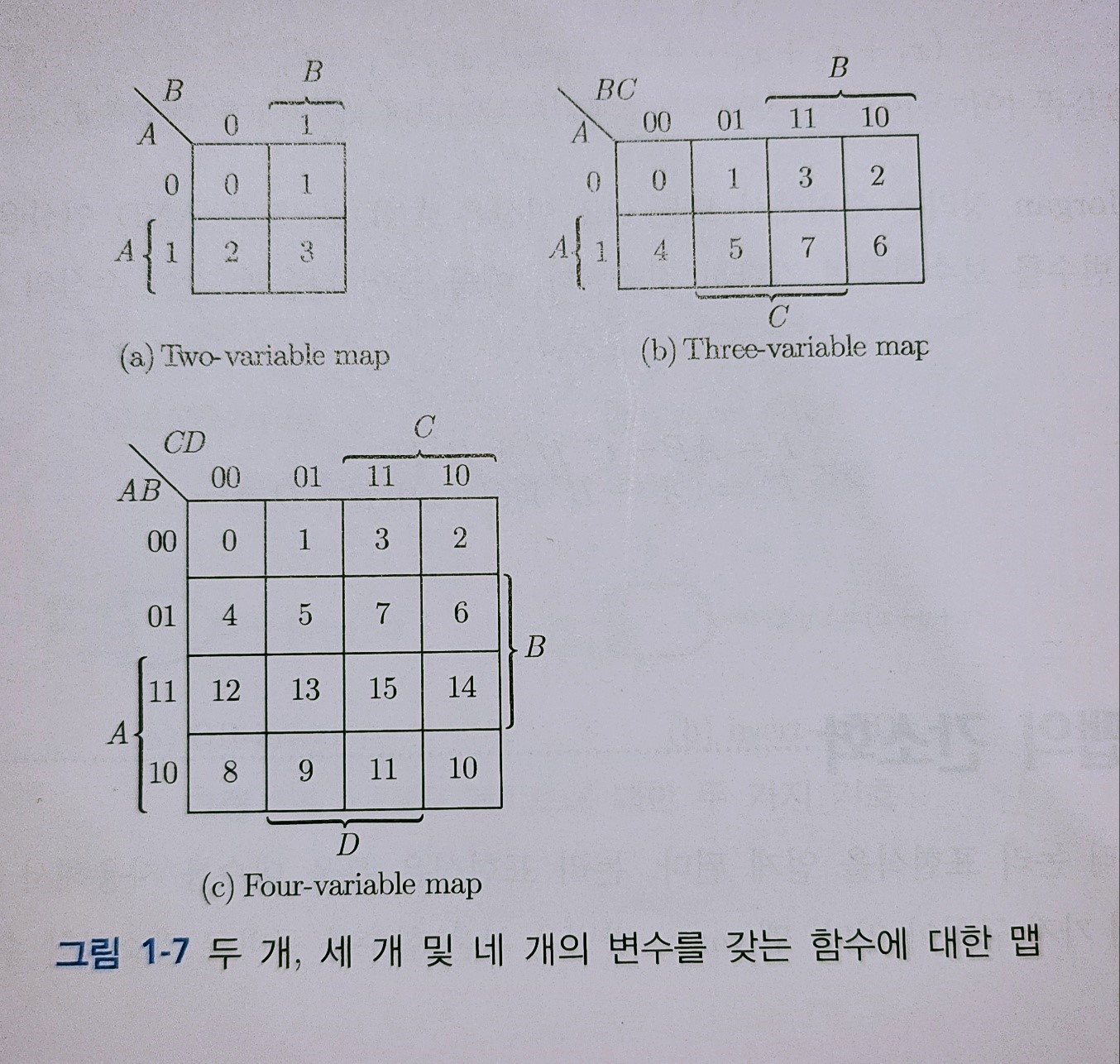
그림 1-7

• <그림 1-7>은 변수가 2개, 3개, 4개인 함수의 Map을 표시

• 구역 안의 숫자는 진리표의 위에서 부터 몇번째의 minterm 인가를 보여주는 숫자(minterm 번호)0,1,2,3,…을 넣는다.

• 진리표에 의해 표시되는 부울대수는 그 함수의 값이 1이 되는 minterm 을 해당하는 구역에 1을 넣는다.

• 인접 구역의 1을 가능한 크게 묶는다.

• 2,4,8,16,.., 2n 개씩 2의 승수개로 묶는다.

• 묶어낸 각각의 그룹은 대수항으로 표시하고 OR로 연결 SOP(sum of products - 논리곱의 논리합), POS(product of sums - 논리합의 논리곱)

Flip-Flop

• 기능 및 동작
  • 순차논리회로의 기본회로
  • 1-비트를 저장하는 2진 셀(Cell)
  • 정상출력과 보수화된 출력을 갖는다
  • 클럭펄스(Clock Pulse)에 의해 동작을 시작(Trigger)
  • 입력 펄스가 상태 변환을 일으키기 전까지 2진상태를 그대로 유지
  • (ex) clock이 떨어질때 데이터를 바꿈. ┏┓

Logic Circuit

• 조합회로 (Combinational circuits)
  • 입력과 출력을 가진 논리 게이트의 집합
  • 출력의 값은 입력의 0과 1들의 조합의 함수
  • 게이트로만 된 회로
• 순차회로 (Sequential circuits)
  • 게이트뿐만 아니라 플립플롭과 같은 기억회로를 포함

주요 차이점 요약:

구분	조합회로	순차회로
상태 저장	없음 (현재 입력만으로 출력 결정)	있음 (이전 상태 + 현재 입력으로 출력 결정)
메모리 소자	없음	있음 (플립플롭, 래치 등)
출력	즉각적, 현재 입력에 의존	클럭 신호에 의해 이전 상태와 입력에 의존
예시	논리 게이트, 가산기, 디코더	플립플롭, 카운터, 상태기계

순차 회로

• 플립플롭이 포함될 때 순차 회로가 된다.

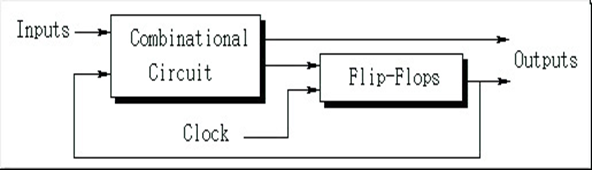
클럭 펄스에 동기되는 순차 회로의 블럭도

• 클럭 펄스에 따라 플립플롭의 출력이 조합회로에 입력된다.
• 플립플롭 입력식
  • 플립플롭의 입력을 만들어내는 조합 회로의 부분
  • 플립플롭의 입력 D는 조합회로의 출력에 연결됨
  • 부울식:
    • DA = Ax + Bx
    • DB = A’x

상태도

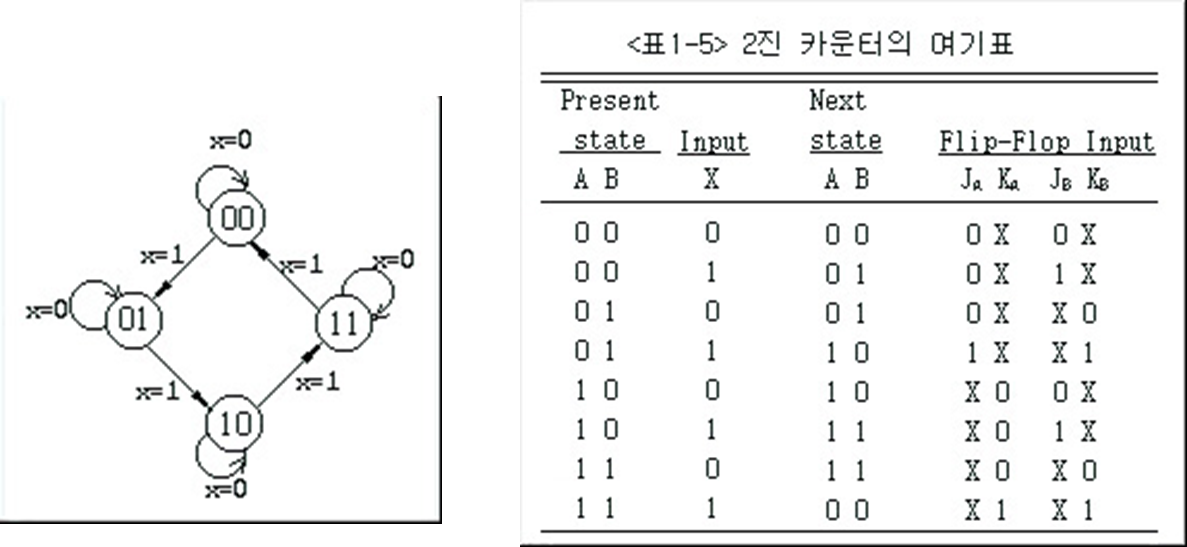
• 상태 00으로부터 01로 가는 직선 위에 표시된 1/0은 입력이 1이고 출력이 0일때 순차회로가 현상태 00에 있음.
• 다음 클럭 펄스가 들어오면 회로는 다음 상태 01로 간다.
• 원에서 나온 선이 자신의 원으로 다시 들어가는 것은 상태의 변화가 일어나지 않음을 의미함.

• 상태가 2비트로 되어있으므로 두개의 플립플롭이 필요하다.

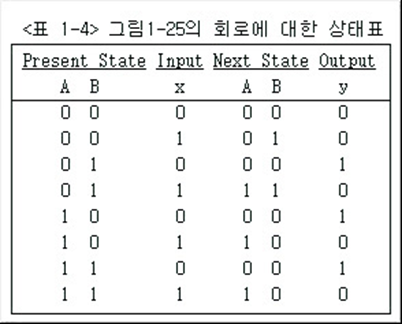
• m개의 플립플롭, n개의 입력변수, p개의 출력 변수를 갖는 순차회로
  • 현상태에 m개의 열, 입력에 n개의 열, 다음상태에 m개의 열, 출력에 p개의 행을 갖는 상태표가 된다